CS154 Spring 2013Practice Midterm 1

To study for the midterm I would suggest you: (1) Know how to do (by heart) all the practice problems. (2) Go over your notes at least three times. Second and third time try to see how much you can remember from the first time. (3) Go over the homework problems. (4) Try to create your own problems similar to the ones I have given and solve them. (5) Skim the relevant sections from the book. (6) If you want to study in groups, at this point you are ready to quiz each other. The practice midterm is below. Here are some facts about the actual midterm: (a) It is closed book, closed notes. Nothing will be permitted on your desk except your pen (pencil) and test. (b) You should bring photo ID. (c) There will be more than one version of the test. Each version will be of comparable difficulty. (d) One problem (less typos) on the actual test will be from the practice test.

1. Let `P = {P_1, ..., P_m}` be a partition of a set `X`. Suppose `\bar P = {bar{P}_1, ..., bar{P}_m}` is also a partition of `X` (bar being complement with respect to `X`). What are the possible values of `m` and why?
2. Give an example of relation `R` which is reflexive and transitive but not symmetric.
3. Suppose we have a graph `G = (V, E)` where `V = {v_1, ..., v_n}` and `E = {(v_1, v_2), (v_2, v_3), ... , (v_(n-1), v_n), (v_n, v_1)}`. Explain step-by-step how the simple path algorithm from class would run on this graph together with the input vertices `s=v_1` and `t=v_(lfloor n/2 rfloor)`.
4. Consider the language `L = {w | w in {0,1}^\star mbox{ has an even number of substrings of the form 01}}`. Draw a DFA state diagram for this language. Then write your DFA down as a 5-tuple.
5. Give an `O(n)` algorithm written in Java for determining if a string is in the language `L` of the previous problem. Prove it is `O(n)` up to a set of justifiable assumptions that you state. We need some assumptions because of things like int's in Java being 32-bit, etc.
6. Let `L' = {w | w in {0,1}^\star mbox{ has an odd number of substrings of the form 10}}`. Use the Cartesian product construction to build an automata for `L cap L'` where `L` is the language of the previous two problems.
7. Consider the language `{0,1}^star 1 {0,1}^(k - 1)`. Give a `k+1` state NFA for this language. Suppose one applied the power set construction to this NFA, show the number of states reachable from the start state in this machine is `2^k`.
8. Let `L` be a language consisting of a single string of length `n`. Prove that there is a DFA for this language. Then argue that a minimal DFA for this language needs at least `n` transitions. (So DFAs are not so great for compression of single strings, people do consider NFA transducers with advice though). Suppose we had a language `L'` with two strings of length `n` show that it is possible for `L'` to have fewer than `2n` states.
9. Consider the DFA
   
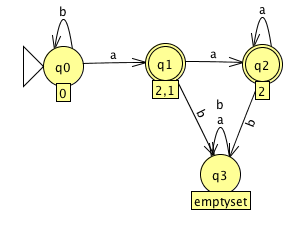
   Show step-by-step how the state minimization procedure from class would act on this automaton to build a minimal equivalent one.
10. Suppose `L = L(M)` for some DFA `M = (Q, Sigma, delta, q_0, F)`. Give the 5-tuple of an NFA recognizing `L^+`.